SOLUCIONARIO DE EXAMEN DE MATEMATICAS

SOLUCIONARIO DE EXAMEN DE MATEMATICAS  POR EL PROFE MATEFACIL (ALIPIO)
1) Calcula, utilizando la definición de logaritmo:
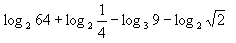
Solución

2) Resuelve:
Solución

3) De un triángulo rectángulo se sabe que su área vale 864 cm² y un cateto mide 48 cm. Calcula las razones trigonométricas de sus ángulos.
Solución

4) Sabiendo que sen x = 2/3 y que 0 < x < 90º, calcula sen 2x y
cos (30º – x) utilizando las fórmulas del ángulo doble y de la diferencia de ángulos.
Solución

5) Calcula, expresando en forma polar:
Solución

6) Dados los vectores a(3, –2), b(–1, 2) y c(0, –5), calcula m y n de manera que: c = m a + n b
Solución

7) Determina k para que los puntos A(–3, 5), B(2, 1) y C(6, k) estén alineados.
Solución

8) Representa:
Solución

9) Calcula el límite:
Solución

10) Halla los puntos de tangente horizontal de la función:
y = x³ – 3x² – 9x – 1
Solución

PROBABILIDADES T. BAYES

Problema 01
En una clase, el 55% son chicos y el 45% restante chicas. En el examen de una asignatura, han aprobado el 80% de los chicos y el 90% de las chicas.
1) Calcula la probabilidad de que al elegir un estudiante al azar, haya aprobado.
2) Sabiendo que un estudiante ha aprobado, calcula la probabilidad de que sea chica




Problema 02
Consideremos el experimento Aleatorio de lanzar una moneda tres veces al aire. 1) Calcular el espacio muestral. 2) Calcular la probabilidad de obtener tres caras. 3) Calcular la probabilidad de obtener una cara.





Problema 03
Un software detecta que el 1% de los usuarios legitimos hace al dia llamadas que se originan en dos ó mas areas metropolitanas. sin embargo 30% de los usuarios fraudulentos hacen llamadas de dos ó mas áreas metropolitanas. La proporcion de usuarios fraudulentos es de 0.01%. Si el mismo usuario hace en un dia llamadas desde dos ó mas áreas. ¿Cuál es la probabilidad de que sea fraudulento?



PROFE: MATEFACIL

INTEGRACION POR PARTES

El método de integración por partes se basa en la derivada de un producto y se utiliza para resolver algunas integrales de productos.

Tenemos que derivar u e integrar v', por lo que será conveniente que la integral de v' sea inmediata.

Las funciones polinómicas, logarítmicas y arcotangente se eligen como u.

Las funciones exponenciales y trígonométricas del tipo seno y coseno, se eligen como v'.

PROBLEMAS RESUELTOS